12.9. приближенное вычисление определенных интегралов
12.9. приближенное вычисление определенных интегралов
На практике часто встречаются интегралы, которые не выражаются через элементарные функции или выражаются очень сложно. Нередко подынтегральная функция задается таблицей или графиком. В этих случаях интегралы находят численными методами. Основа численных методов построения формул приближенного вычисления интегралов состоит в замене частичных криволинейных трапеций, образующихся при разбиении отрезка интегрирования, на более простые фигуры. В формуле прямоугольников — это прямоугольники; в формуле трапеций — трапеции; в формуле парабол — параболы. Рассмотрим эти методы более подробно.
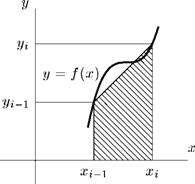
Формула прямоугольников. Пусть на отрезке [а, Ь] задана функция у = f(x). Требуется вычислить площадь криволинейной трапеции S, ограниченной кривой у = f(x) и прямыми х = а, х = b и у = О (рис. 12.1).
Ранее было дано определение интегральной суммы. Напомним, как она строилась. Отрезок [а, Ь] разбивался на п промежутков точками жо, жі, ..., хп:
а = хо < х < Х2 < ... < xn-i < хп = Ь.
На каждом отрезке разбиения выбиралась точка С{ и полагалось
Ах і — х{ х{—\^ і — . 2, л.
Тогда произведение f(ci)Axi представляло площадь прямоугольника Si со сторонами f(ci) и Ах і. Сумма площадей всех таких прямоугольников равнялась сумме вида
п г=1
причем Sn можно было считать приближенно равной искомой площади S.
Формула прямоугольников практически совпадает с приближенной формулой для определенного интеграла
b
п
f(x)dx » Sn = ^2f(a)Axi.
Отличие состоит лишь в том, что в формуле прямоугольников меньше произвола. Отрезок [а, Ь] делится на равные части (а не
произвольным образом, как в определении определенного интеграла), а значения с{ представляют середины соответствующих
ОТреЗКОВ [#г-Ъ хгИтак, формулой прямоугольников называется следующее приближенное равенство:
f(x)dx
(У1 + У2 + ... + Уп),
где
— — длина каждого отрезка, а у і = f (с«), с{ — середина її
отрезка [xi-i, Х{].
С увеличением п точность формулы неограниченно возрастает. В пособиях по численным методам доказывается, что предельная погрешность Rn = |S — Sn формулы прямоугольников составляет
(Ь
24п2
М2,
(12.1)
где М2 — наибольшее значение |//7(ж)| на отрезке [а, 6]. Для эмпирических функций вместо М2 берут наибольшее значение
|А2И
величины
Ах2
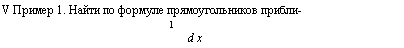
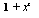 женное значение интеграла Решение. Имеем
женное значение интеграла Решение. Имеем
о
(= j = 0,785398...).
| Cl | = 0,05 | Ш | = 0,9995, |
| С2 | = 0,15 | т | = 0,9780, |
| сз | = 0,25 | т | = 0,9442, |
| С4 | = 0,35 | ш | = 0,8909, |
| С5 | = 0,45 | Уь | = 0,8316, |
| Сб | = 0,55 | Уб | = 0,7678, |
| С7 | = 0,65 | У7 | = 0,7029, |
| С8 | = 0,75 | ш | = 0,6400, |
с9 = 0,85 сю = 0,95
У9 = 0,5806, Шо = 0,5256,
откуда
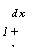 dx
dx
Л.уюу = 1.7 8581. ^ у 10 '
Погрешность — — 0,78581 составляет примерно 0,0004. Вычислим теоретическую предельную погрешность. Имеем:
23 '
Зж2 1
/"(*) = 2
Наибольшее значение на отрезке [0, 1] равно 2 (оно достигается при х = 0). Подставляя п = 10, М2 = 2 в формулу для предельной погрешности (12.1), получим Rio = 0,00085 (она никогда не превысит действительную погрешность). Значит, нет смысла вычислять ~yl больше чем на четыре знака. А
Формула трапеций. Формула трапеций также представляет приближенную формулу вычисления определенного интегра-Ъ
ла J f(x) dx.
а
Приближенное значение искомого интеграла можно получить, заменив площадь под кривой площадью под ломаной, расположенной достаточно близко к исходной кривой. Для построения этой ломаной разобьем отрезок интегрирования на п равных
частей длиной h = -—и на каждом отрезке разбиения [#г-ъ xi]
заменим часть кривой у = f(x) хордой, соединяющей концевые точки (рис. 12.13). Тогда
f(x) dx я S± + S2 + ... + Sn,
где Si, #2, ••• 5 Sn — площади трапеций (площади под хордами на каждом из отрезков разбиения). Площадь каждой трапеции Si
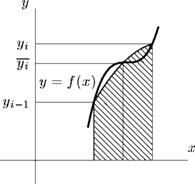
Хі — Сі Хі
а б
формула трапеций формула парабол
Рис. 12.13. Приближенные формулы
„ f{Xi-i) + f(Xi)
равна полусумме основании , умноженный на вы-
соту h =
b — а
Обозначим f(x{) через у і. Тогда
s. = y_izl±yih
и Ъ
f(x)dx « S± + S2 + ... + Sn =
-ь(У^мУ±мУ±мУ1л, Уп-1 , Уп
" V2 + 2 + 2 + 2 2 2 /
Все слагаемые, кроме крайних Щи встречаются дважды.
Поэтому окончательно получаем формулу трапеций:
/(я) Же и ^ + уі + у2 + ... + уп_2 + + Ні
9 Я. М. Ахтямов
значение интеграла
V Пример 2. Найти по формуле трапеций приближенное і
dx (= J = 0,785398...).
l + xz
о
Решение. Имеем
| х0 = 0,0 | уо = 1,0000, |
| xi = 0,1 | Уі = 0,9901, |
| х2 = 0,2 | у2 = 0,9615, |
| х3 = 0,3 | уз = 0,9174, |
| Ж4 = 0,4 | у4 = 0,8621, |
| Ж5 = 0,5 | у5 = 0,8000, |
| Жб = 0,6 | Уб = 0,7353, |
| хч = 0,7 | У7 = 0,6711, |
| xs = 0,8 | у8 = 0,6098, |
| Хд = 0,9 | у9 = 0,5525, |
| хю = 1,0 | 2/ю = 0,5000, |
откуда і
dx
1 + х2
dx ~
b — а
п
1,5000
+ 7,0998 = 0,78498.

Ь а ҐУо + Уг, Зп
+ (уі + ...+Уп-і) + 2(т + ---+Уї)
СЙМПСОН (Simpson) Томас (1710-1761) — английский математик, член Лондонского королевского общества. Был ткачом шелковых тканей, математику изучил самостоятельно. Основные труды по геометрии, тригонометрии и математическому анализу. Вывел формулу приближенного интегрирования (формулу Симпсона). Один из основоположников теории ошибок.
В основе этого метода лежит замена частичных криволинейных трапеций, ограниченных сверху функцией / (ж), на криволинейную трапецию, ограниченную сверху параболой вида
у = Ах2 + В х + С.
Предельная погрешность формулы Симпсона составляет
Здесь М4 — наибольшее значение |/^4^| на отрезке [а, Ь].
V Пример 3. Найти по формуле Симпсона приближенное і
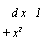 |
(= ^ = 0,785398...).
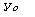 о
о
Решение. Имеем
х0 = 0,00
сі = 0,25 xi = 0,50 с2 = 0,75
х2 = 1,00
2 Уі
і
У 4 =
0,50000,
1,88235, 0,80000, 0,28000,
0,250000,
откуда
dr 1
dx&-4,71235 = 0,78539. 1 + ж2 6
Погрешность составляет примерно 0,00001, т. е. в 40 раз меньше, чем в примерах 1 и 2, хотя там число ординат было вдвое больше.
Численное вычисление на компьютере. Используя какой-либо из методов, описанных выше, и формулу предельной погрешности соответствующей формулы, можно вычислять определенные интегралы с любой степенью точности. В Maple для этого существует команда:
>evalf(Int(expr,х=а..b,digits);
Здесь обязательными параметрами являются подынтегральная функция ехрг, зависящая только от переменной х, а и b — пределы интегрирования, а необязательным — digits — точность вычисления.
V Пример 4. С помощью пакета Maple найти с точностью і
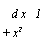 |
(= j = 0,785398...).
>evalf(Int(l/(l+x~2),х=0..1,3);
і
7^ = 0,785. А
1 + X
до 10 4 интеграл Решение.
V Пример 5. С помощью пакета Maple найти с точностью і
sin х dx
>evalf(lnt(sin(x)/x,x=0..1,4);
і
sin х dx
= 0,9461.
sin X
Заметим, что функция не интегрируема в элементарных
X
функциях. А
Обсуждение Математика для социологов и экономистов
Комментарии, рецензии и отзывы
