11.3. непосредственное интегрирование

11.3. непосредственное интегрирование

Всякая формула дифференцирования, рассмотренная в обратном порядке, дает формулу интегрирования, например:

(е2ж + cos ж)' = 2е2ж sin ж,

(2 е2х sin х) dx = е2х + cos х + С.

Таким образом, из таблицы производных нетрудно получить таблицу интегралов (см. следующую страницу).

Справедливость каждой формулы проверяется непосредственно дифференцированием.

Например, формула 1 верна, так как (х + С)' = х' + С = 1.

Формула

Таблица интегралов

/0*0

f{x)dx

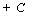1

ха (а ф -1)

х + С

„а+1

а + 1

3

4

ех + С ах/1па + С

— (ха, а = х

-1)

In х + С

ж In а

oga х + С

COS X

sin X

sin х + С cos х + С

9

10

cos2 x

sin2 ж

tgx + C -ctgx + С

11

12

Va2-,

(a > 0, —a < x < a) (а ф 0)

/ x2 + a

In

arcsin —hC a

с + л/ж2 + а

+ C

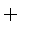
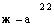ж + а

(а^О)

arctg — + С

х — а

х + а

J-ln

2а

следует из равенства

1

ка + 1 у а + 1 Докажем равенство

■ ж

а+1 _

-(« + 1)жа =Жа.

— б/ж = In х + С.

x

Пусть х > 0. Тогда |ж| = х и (In |ж| + С)' = (пх + С)' = —

Если х < 0, то |ж| = —х и (In |ж| + С) = (1п(—х) + С) = — = = 1,Т.,в„6о„хслуЧаях„Ро„зводНаярМ„а1

x x

Аналогично доказываются остальные формулы.

Интегрирование, основанное на прямом использовании таблицы интегралов, называется непосредственным интегрированием.

При непосредственном интегрировании могут представиться следующие случаи:

данный интеграл находится непосредственно по соответствующему табличному интегралу;

данный интеграл после применения свойств 4 и 5 приводится к одному или нескольким табличным интегралам;

3) данный интеграл после элементарных тождественных

преобразований над подынтегральной функцией и применения

свойств 4 и 5 приводится к одному или нескольким табличным

интегралам.

Рассмотрим три примера, каждый из которых соответствует одному из трех случаев непосредственного интегрирования.

dx,

1

* 1 4

V Пример 1. Найти х3 dx, —dx, f Vx^ dx,

J x J

dx.

Решение. Все пять интегралов имеют вид: |жа dx. В первом

случае а = 3, во втором а = —3, в третьем а = 5/4, в четвертом а = —5/4 и в пятом а = — 1. В первых четырех случаях а ф — 1, поэтому применяем формулу 2:

^ск+1

ха dx =

а + 1

+ с.

5 5 При а. = 3. а. = —3, а = и а = — имеем:

4 4

—г dx =

х6

X

х

3+1

х3 dx =

3 + 1

-3+1

dx =

-3 + 1

+ с

+ С-

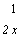
^2+ С,

хъ dx —

х4 dx =

х

+ С = ^+ С =

4

+ С,

dx =

4+i

х 4 dx = + С = ^—r + С = --^= + С.

-+ 1 -Ух

В следующем примере формулу 2, с помощью которой были найдены предыдущие интегралы, использовать нельзя, так как а = — 1. Но этот интеграл также является табличным (формула 5):

х 1 dx =

— dx = In х + С. А

— ) dx.

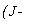
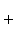
V Пример 2. Найти

\Ґх 5 cos2(ж) ж, Решение. Используя свойства 4 и 5 и формулы 2,5,9, имеем:

+

(.

V у/х 5 cos2 (ж) х

dx = 3

1

W+ 5 dx

cos (ж)

-2

х

= 3^— + і tga;-2 lnx + C = -5 + 1 5

= 4,5 ¥x* + tgx 2 In ж + С. A

5

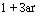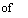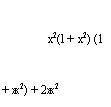
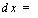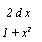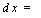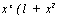
V Пример 3. Найти

Решение.

1 + Зж2

x2(l + x2)

(1 + х2)

dx +

xz(l + xz

dx , —dx +

dx =

= + 2 arctg ж + С. A

Задача. Найти неопределенный интеграл Результат проверить дифференцированием.

Г3-2ж4+ у/х2

dx.

Ответ: 4 Vx^ — ¥х^ + Х\[х^ + С. 19 17