2.2. элементарные функции

2.2. элементарные функции

Сложная функция. Пусть функция у = f(u) есть функция от переменной и, определенной на множестве U с областью значений У, а переменная и в свою очередь является функцией и = д(х) от переменной ж, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция у = f(g(x)) называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции).

Например, у = sm(x2 + 1) — сложная функция, так как она составлена из двух функций у = sin и и и = х2 + 1.

Разумеется, сложную функцию можно составлять и из большего числа функций. Например, функция у = In (sm(x2 + 1) составлена из трех функций у = In г>, v = sin и и и = х2 + 1.

Понятие элементарной функции. Из основных элементарных функций новые функции могут быть получены двумя способами при помощи:

а) алгебраических действий;

б) операций образования сложной функции.

Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Функция

у = х2 + sin х

является элементарной, так как она получена из основных элементарных функций: степенной х2 и тригонометрической sin ж с помощью операции сложения. Функция

у = 3х — х • In х

получена из функций: показательной Зж, степенной х и логарифмической In ж с помощью операций вычитания и умножения. Поэтому она — элементарна.

Элементарна также сложная функция

у = sin ж6,

степенной ж6 и тригонометрической sin ж.

которая образована из двух основных элементарных функций: пенной ж6 Функция

у = Vsin х —

2х

In (х cos х + 4)

получена из основных элементарных функций у = л/х , у = sin ж, у = 2х. у = 1, у = In ж, у = ж2, у = cos х с помощью алгебраических действий сложения, вычитания, умножения, деления и операции образования сложной функции. Поэтому она является элементарной.

Примерами неэлементарных функций являются функция Дирихле и функция у = [х]. Функция Дирихле

у(х) = °i

О, если х — иррациональное число, если х — рациональное число

определена на всей числовой прямой, множество ее значений состоит из двух точек: 0 и 1. График ее изобразить невозможно. На рис. 2.21 приведено лишь схематическое изображение этой функции.

у 3 2

у 3 2

1

н

-1 О

-1

х

Л О

Рис. 2.21. Функция Дирихле и функция у = [х]

ДИРИХЛЕ (Dirichlet) Петер Густав Лежён (1805-1859) — немецкий математик, член Берлинской Академии наук. С 17 лет в течении 5 лет был домашним учителем в Париже. В 22 года — доцент в Бреславле. В 26 лет — профессор Берлинского университета. После смерти К. Гаусса (1855) — профессор Гетингенского университета. С именем Дирихле связаны задача, интеграл, принцип, функция, ряды и многое другое. Его лекции имели огромное влияние на выдающихся математиков более позднего времени.

Функция у = [х] (читается «у равно антье х») — целая часть от значений аргумента — задана для всех вещественных значений ж, а множество ее значений состоит из целых чисел. Ее график изображен на рис. 2.21.

Название элементарных функций сложилось исторически. В процессе развития математики и ее приложений элементарные функции появились сравнительно рано и играли важную роль, поэтому и символы, введенные для их обозначения, как, например, sin ж, стали хорошо известными и привычными. Но с точки зрения современной математики нет никакого основания называть элементарные функции более простыми , чем неэлементарные. Например, элементарная функция

2х -3

у

sin x*

In (х2 ^/cosx + 4)

не выглядит проще неэлементарной функции у = [х].

3. Преобразования графиков функций. Покажем, как из графика функции у = f(x) можно получить графики функций вида

у = Af(ax + b) + В, где Л, В, a, b — некоторые действительные числа.

1. График функции у = f(x) + b получается из графика функции параллельным переносом.

у /

д А Если b > 0, то перенос совершается

д /J параллельно оси ординат на расстояние b

\ // вверх, а если b < 0, то вниз на расстоя / ниє На рис. 2.22 изображены графики

—і—і—і ч--^ і—і—г— функций у = х2 (пунктирной линией) и

у = х2 + 1 (сплошной линией).

Рис. 2.22

2. График функции у = f(x + а) также получается из графика функции у = f(x) параллельным переносом.

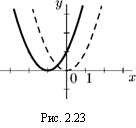
Если а > 0, то график переносится параллельно оси абсцисс влево на расстояние а, а если а < 0, то вправо на расстояние а. Нарис. 2.23 изображены графики функций у = х2 (пунктирной линией) и у = (х + I)2 (сплошной линией).

3. График функции у = Af(x), где Л > 0, получается из графика функции у = f(x) растяжением или сжатием вдоль оси ординат.

Если А > 1, то график функции растягивается вдоль оси Оу в Л раз, а если 0 < Л < 1, то сжимается в 1/Л раз. На рис. 2.24 изображены графики функций у = sin х (пунктирной линией) и у = 2 sin ж (сплошной линией).

График функции у = /(а ж), где а > О, получается из графика функции у = f(x) сжатием к оси ординат или растяжением вдоль оси абсцисс.

у

лл1

Рис. 2.25

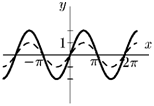
График функции у = f(ax) есть график у = f(x), сжатый (при а > 1) в а раз или растянутый (при 0 < а < 1) вдоль оси Ох. На рис. 2.25 изображены графики функций у = sin х (пунктирной линией) и у = sin 2х (сплошной линией).

График функции у = —f(x) получают из графика функции у = f(x) зеркальным отражением относительно оси абсцисс.

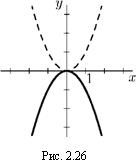На рис. 2.26 изображены графики функций у = х2 (пунктирной линией) и у = —х2 (сплошной линией).

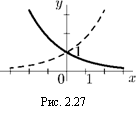6. График функции у = f(—x) получается из графика функции у = f(x) зеркальным отражением относительно оси ординат.

На рис. 2.27 изображены графики функций у = ах, где а > 0 (пунктирной линией) и у = а~х (сплошной линией).

7. Рассмотрим теперь, как получается график функции y = Af(ax + b) + B, где А > 0 и а > 0, из графика функции у = f(x). Так как

y = Af(a (х + Ь/а))+В,

то сжатием вдоль оси абсцисс получим график функции у = = f(ax). Из этого графика сжатием вдоль оси ординат получим график функции у = Af(ax), из которого параллельным переносом вдоль оси абсцисс на Ь/а единиц и вдоль оси ординат на В единиц получим график функции у = Af(ax + b) + B.

Работайте, работайте, — полное понимание придет потом.

Даламбер