12.10. несобственные интегралы

12.10. несобственные интегралы

Понятие определенного интеграла было введено для функции, ограниченной на отрезке [а, Ь]. Ряд конкретных задач (в частности, задач теории случайных величин) приводит к расширению понятия интеграла на случаи бесконечных промежутков и разрывных функций. Такие интегралы называются несобственными. Различают несобственные интегралы первого и второго рода в зависимости от того, имеем ли мы дело с бесконечным промежутком интегрирования или с неограниченной подынтегральной функцией.

Несобственные интегралы первого рода. Пусть функция у = f(x) непрерывна при х ^ а.

Определение 1. Если интеграл

f(x)dx

(12.2)

при b —> +оо имеет конечный предел, то этот предел называется несобственным интегралом функции f(x) от а до бесконечности и обозначается

f(x)dx.

Итак, по определению

f(x) dx = lim

f(x)dx.

(12.3)

Если интеграл (12.2) при b —> +oo имеет бесконечный предел или вовсе не имеет предела, то говорят, что несобственный интеграл (12.3) расходится. Если интеграл (12.2) при b —> +оо имеет конечный предел, то говорят, что несобственный интеграл (12.3) сходится.

V Пример 1. Найти J 2 х dx.

Решение. Имеем

2 х dx = lim

2~xdx = lim -1-(-2-ж)16 Ь_>+00 In 2 v J

= iim _L (l L = _L (l -0) = -L ~ 14. b^+oo In 2 V 2b J In 2 v J In 2

= і

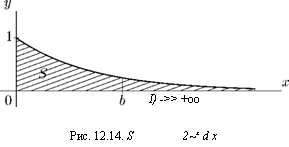
Геометрическое истолкование. Интеграл J 2 х dx изображао

ется криволинейной трапецией, ограниченной линиями у = 2_ж, у = О, ж = О, х = b (рис. 12.14). По мере удаления b от начала координат площадь криволинейной трапеции возрастает, но не безгранично. Она стремится к 1/1п2. Таким образом, площадь бесконечной области под линией у = 2~х конечна (равна 1/ In 2). Это не удивительно. Объяснить это можно следующим образом. Площадь бесконечного луча на плоскости равна нулю (у луча нет ширины), т. е. тоже конечна. При добавлении к лучу треугольника получается бесконечная фигура, которая имеет конечную ненулевую площадь. Примерно то же самое и с несобственным интегралом. По мере удаления b от начала координат бесконечная область под линией у = 2~х настолько сближается с осью абсцисс, что почти сливается с ней. В результате площадь всей фигуры оказывается конечной. Функция у = 2~х сродни также геометри-

ческому ряду Y1 2"

п=0

который имеет конечную сумму. А

Геометрический смысл несобственного интеграла (12.3) для неотрицательной на [а, +оо) функции f(x) состоит в том, что он представляет собой площадь криволинейной фигуры, ограниченной данной линией у = /(ж), осью Ох и вертикалью х = а.

V Пример 2. Найти

г dx

J х l

Решение. Имеем

+оо b

dx Л.

— = Inn

x +

dx л. л — = I mi In x

x Ь^ + og

= lim (In b

■0) = +oo.

Значит, искомый несобственный интеграл расходится. Геометрически это означает, что площадь области под гиперболой у = —

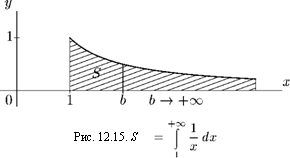x

неограниченно возрастает (по мере удаления b от начала координат гипербола недостаточно приближается к оси Ох, чтобы площадь была конечной). А

Пусть функция непрерывна в промежутке (—оо, Ь].

Определение 2. Несобственным интегралом функции f(x)

ъ

от —оо до а называется предел интеграла J f(x) dx при а —> —оо:

f(x) dx = lim

f(x) dx.

Сходимость и расходимость несобственного интеграла J / (х) dx

— оо

понимаются как в определении 1.

Пусть функция непрерывна на всей числовой оси.

Определение 3. Несобственным интегралом функции f(x) от —оо до +оо называется следующая сумма:

+ 00

+ 00

f(x)dx =

f(x)dx +

f(x)dx.

Она не зависит от выбора точки х = с. Предполагается, что оба

несобственных интеграла сходятся. Интеграл J f(x)dx выра— оо

жает площадь области под линией у = f(x), бесконечно простирающейся в обе стороны.

V Пример 3. Найти площадь бесконечной области под лини-d3

ей у

локон Аньези (рис. 12.16).

dz + xz

АНЬЁЗИ (Agnesi) Мария Гаэтана (1718-1799) — итальянский математик, профессор университета в Болонье. Родилась в Милане. В

d3

ее честь плоскую кривую, выраженную уравнением у = —^

назвали «локон Аньези».

Решение. Искомая площадь представляется интегралом

+оо 0 +оо

d<

dz + x2

dx =

dc

dz + x2

dx +

d<

d2 + xz

dx.

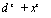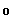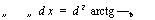TO

—T dx = lim d2 arctg —t = n d212.

d2 + x2 b^+oc d

Аналогично о

—dx = — lim d2 arctg = тг d212,

d2 + x2 a^-oo ° d 1

откуда

dx = тг d2.

Таким образом, площадь искомой бесконечной фигуры вчетверо больше площади круга с диаметром d. Этот результат получила итальянский математик Мария Аньези. (Впрочем, еще за сто лет до Аньези искомую площадь другим методом нашел Ферма.) А

Иногда вместо lim F(b) пишут F(±oo). Такая запись поз6—)>±ос

воляет обобщить формулу Ньютона-Лейбница. Действительно, пусть F(x) — первообразная функция для непрерывной функции f(x). Тогда

f{x)dx =

f(x)dx +

f(x)dx =

= lim (F(b) F(c)) + lim (F(c) F(a)) =

b—>+oc a—> — oo

= lim F(b)- lim F(a) = F(+oo) F(-oo).

Таким образом, если функция f(x) непрерывна на всей числовой оси, то формула Ньютона-Лейбница

f(x) dx = F(b) F(a) верна и в случае, когда а или b равны ±оо.

V Пример 4. Найти несобственный интеграл

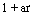dx.

Решение.

1 0

dx — arctg х

1 + x

7Г 7Г

arctg0 — arctg (—оо) = 0 —(— — ) = —. А

Несобственные интегралы второго рода.

Определение 4. Пусть функция f(x) непрерывна при а < х ^ b и имеет точку разрыва при х = а. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой

fix) dx = lim

f(x)dx

(12.4)

a+e

и называется сходящимся или расходящимся в зависимости от того, существует или не существует предел правой части равенства (12.4).

Аналогично определяется несобственный интеграл, когда f(x) имеет разрыв только на конце х = b промежутка [а, Ь).

і

этому і

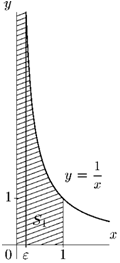
V Пример 5. Найти несобственный интеграл — dx.

Решение. Функция f(x) = — разрывна в точке х = 0. По-

— dx = lim

x є->-+0

1 . 1

— dx = lim (In x) = 1 — (—oo) = +oo.

x £->+ov 7 +£ v 7

0 +£

Искомый несобственный интеграл расходится. Геометрически это означает, что соответствующая криволинейная трапеция («бесконечный шпиль») имеет бесконечную площадь (рис. 12.17). А

Если существует функция F(x), непрерывная на отрезке [а, Ь] и такая, что

F'(x) = f(x) при а < х ^ b

Рис. 12.17. Геометрический смысл несобственного интеграла

{обобщенная первообразная), то для несобственного интеграла (12.4) справедлива обобщенная формула Ньютона-Лейбница:

fix) dx = lim

f(x)dx= Hmo (F(b)-F(a + є)) =

а+є

= F(b) F(a) = F(x)

Таким образом, формула Ньютона-Лейбница для определенных интегралов доказывается] для несобственных она принимается за определение.

Аналогично определяется несобственный интеграл, когда f(x) имеет разрыв только на конце х = b промежутка [а, 6):

f(x) dx = F(b) F(a) = F{x)

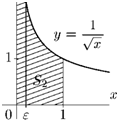
V Пример 6. Найти несобственный интеграл

dx.

Решение. Функция f(x) = —= разрывна в точке х = 0.

л/х

Поэтому

—j=dx = 2 \[х

л/х

= 2-0 = 2.

Геометрически это означает, что соответствующая криволинейная трапеция («бесконечный шпиль») имеет площадь равную двум (рис. 12.17). По сравнению с предыдущим примером площадь оказалась конечной. Это является следствием того, что

«шпиль» для функции у = —=является тонким и, начиная с

л/х

некоторой высоты, почти сливается с осью Оу. А Решение примеров 4, 5, 6 в пакете Maple.

>int(1/(1+х**2),x=-infinity..0);

Ответ: 7Г. 2

>int(l/x,x=0..1);

Ответ: оо.

>int(l/sqrt(x),х=0..1);

Ответ: 2.

Нет ни одной области страктна она ни была, окажется применимой к го мира.

математики, как бы аб-которая когда-нибудь не явлениям действительно 

Н. Лобачевский