19.2. система линейных дифференциальных уравнений с постоянными коэффициентами
19.2. система линейных дифференциальных уравнений с постоянными коэффициентами
Из линейных систем (19.5) наиболее важными, как в теории, так и в приложениях, являются системы с постоянными коэффициентами:
' dyi р /
-j= Pll Уі + Р12 У2 + -.. + Ріп Уп + /і (ж),
^7 = Р21 Уі + Р22 У2 + -.. + Р2п Уп + g б^
dyn dx
= Pnl Уі + Рп2 У2 + -.. + Рпп Уп + fn{x),
где функции fi(x) (і = 1, 2, ... , n) обычно предполагаются непрерывными в некотором интервале X.
Если все (ж) = 0, то система (19.6) называется однородной, в противном случае — неоднородной.
В матричной форме однородная система выглядит следующим образом:
| /1/1 | /Рп | Р12 • | • Р1п | /3/1 | |||
| d | У2 | Р21 | Р22 • | • Р2п | У2 | ||
| dx | |||||||
| Уп/ | Рп1 | Рп2 • | • Рпп/ | Уп) |
По-другому ее можно записать в следующем виде:
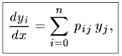 |
В более компактной форме последнюю формулу можно записать так:
dY
dx
(19.7)
где Y =
(уЛ
У2
искомый вектор, а Р — численная матрица
Уп/
размера п х п.
Чтобы найти решение системы (19.7), введем пробную функцию
Y = Ze
к х
где
Z =
Подставим ее в левую часть равенства (19.7). Получим
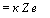 dY _ d(Zekx)
dY _ d(Zekx)
dx dx Отсюда и из (19.7) вытекает, что
PZekx = kZekx
к х
или
Р Z = к Z.
Полученное уравнение — это уравнение на собственные векторы квадратной матрицы. Использование единичной матрицы Е дает уравнение на собственные числа квадратной матрицы
det(PкЕ) = 0,
которое называется характеристическим уравнением.
Если все п корней kj характеристического уравнения различны и Zj — соответствующие вектора матрицы Р, то общее решение системы (19.7) имеет вид
Y = J2CjZjek^,
г=0
где j = 1, 2, ... , п.
V Пример 1. Найти общее решение однородной автономной системы
dy2 dx
= 2yi + У2.
= 0;
Решение. Решаем характеристическое уравнение
1-к 2
det(P-kE) =
1-к
(1-к)2 -4 = 0; &i = -l, к2 = 3. Общее решение имеет вид
У = Ci Zie-x + C2Z2 е3х. Для определения собственного вектора
Zi =
*12.
соответствующего собственному значению к = —1, решаем систему
PZx = kx Zi, которую можно записать так:
Отсюда или
/2(^11 + ^12) = 2(2Г11 + z12)J
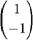
Так как определитель этой системы равен нулю, то система имеет бесчисленное множество решений. В данном случае можно выбрать zu = 1, a Z12 = — 1, т. е. можно считать, что
Zi =
Для определения собственного вектора
соответствующего собственному значению к = 3, решаем систему
PZ1 = fciZi,
которую можно записать так:
<*<'-*»*>=С Г Д) (£)=•■
Отсюда
/2(-z2i + *22)
^2(^21-^22); иТак как определитель этой системы равен нулю, система имеет бесчисленное множество решений. В данном случае можно выбрать z\ = 1, a z±2 = 1, т. е. можно считать, что
Следовательно, общее решение заданного уравнения имеет вид
Ч:;Н(-')™2СЬ
это означает, что
У1 = С1Є-Х + С2е3х, у2 = -СіЄ-х + С2е3х. ▲
Последняя однородная система может быть решена и другим способом — приведением к однородному дифференциальному уравнению второго порядка с постоянными коэффициентами.
V Пример 2. Найти общее решение однородной автономной системы
приведением к дифференциальному уравнению второго порядка.
Решение. Продифференцируем обе части первого уравнения по переменной х:
d2yi _ dyi dy2 dx2 dx dx
Заменим в полученном уравнении правой частью второго уравнения системы:
d2yi dyx ( .
+ 4У1 + 2у2. (19.8)
или
d2yi = dyi dx2 dx
Из первого уравнения системы находим у2:
1 dVi 1 (ла а
У2=2^~2У1(19-9)
Подставим в (19.8) вместо у2 в правую часть (19.9), получим
d2yi dy! fl dy! 1
откуда
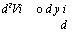 2 -2-^-3У1 = 0.
2 -2-^-3У1 = 0.
dx
Это обыкновенное линейное однородное дифференциальное уравнение. Так как характеристическое уравнение
k2-2k-3 = 0
имеет корни
= -1- &2 = 3,
то
2/1 = Сге-Х + С2е
Зж
(19.10)
Найдем ^ри подставим в (19.9). Получим
^1 = ± (С1Є-Х + С2еЪх) = -С1Є~Х + 3 С2еЪх
1 dyi 1
= I (-Сге-Х + 3 С2е3х) і (С1Є-Ж + С2е3ж) =
= -Сіе-ж + С2е3ж.
Отсюда и из (19.10), получаем
Методом приведения к одному линейному дифференциальному уравнению можно решать и неоднородные системы.
V Пример 3. Найти общее решение неоднородной линейной системы
^ = -8!/i + 3i/2 + 5e-*,
dy2 dx
= -18^/1 + 7у2 + 12е"
приведением к дифференциальному уравнению второго порядка.
Решение. Продифференцируем обе части первого уравнения по переменной X.
d2yi = g гіг/і 3 rig/2 5с-ж
гіж2 гіж гіж
о d2/2
Заменим в полученном уравнении правой частью второго уравнения системы:
= "8 ^ + 3 (-18 уі + 7 у2 + 12 е~х) 5 е"*,
или
Из первого уравнения системы находим у2'» = ї(^+8»-»«-)<1912>
Подставим в (19.11) вместо у2 в правую часть (19.12) и, приведя подобные члены, получим уравнение
Решаем вначале однородное дифференциальное уравнение
d2yi + dyi _ 2 = 0 гіж2 гіж
Так как характеристическое уравнение
&2 + Л 2 = О
имеет корни
Лі = -2, &2 = 1,
то
1/1 одн = СіЄ-2ж + С2ЄЖ.
Пусть уї = А е~х] тогда уї' = — Л е~ж и щ" = А е~х. Подставив эти значения в (19.13), находим Л = 2 и, следовательно,
УГ=2е-*.
Тогда
Уі = Уі од„ + УГ = Сі е"2ж + С2 е* + 2 е"ж. (19.14)
Чтобы найти 2/2 5 продифференцируем обе части последнего равенства:
dyi
1= -2С1е~2х + С2ех -2е~х.
dx
Найденное выражение для подставим в (19.12). Получим
У2 = 2СіЄ-2х + ЗС2еж + 3е"ж. Отсюда и из (19.14), получаем
Задача. Решить систему уравнений
dy_ dx dy2 dx
= 3 yi + 4 y2
двумя способами: 1) с помощью характеристического уравнения; 2) сведением к дифференциальному уравнению второго порядка.
Ответ:
-Г
Обсуждение Математика для социологов и экономистов
Комментарии, рецензии и отзывы
