Глава 20 разностные уравнения 20.1. основные понятия

Глава 20 разностные уравнения 20.1. основные понятия

Разностные уравнения играют большую роль в экономической теории. Многие экономические законы доказывают с помощью именно этих уравнений.

Пусть время t выступает как независимая переменная, а зависимая переменная определяется для времени — 1,£ — 2ит. д.

Обозначим через yt значение в момент времени t; через yt-i — значение функции в момент, сдвинутый назад на единицу (например, в предыдущем часу, на предыдущей неделе и т.п.); через yt-2 — значение функции у в момент, сдвинутый на две единицы назад, и т. д.

Уравнение

«О Уі + «1 Уі-1 + CL2 Уі-2 + + Сіп Уі-п

(20.1)

где ао, аі, ..., ап — постоянные, называется разностным неоднородным уравнением п-го порядка с постоянными коэффициентами.

Уравнение

«0 Уі + «1 Уі-1 + «2 Уі-2 + -.. + Сіп Уі-п = 0,

(20.2)

в котором f(t) = 0, называется разностным однородным уравнением п-го порядка с постоянными коэффициентами.

Решить разностное уравнение п-го порядка — значит найти функцию yt, которая обращает это уравнение в верное тождество.

Решение, в котором отсутствует произвольная постоянная, называется частным решением разностного уравнения; если же в решении есть произвольная постоянная, то оно называется общим решением.

Можно доказать следующие теоремы.

Теорема 1. Если однородное разностное уравнение (20.2) имеет решения yi(t) и г/2(^)? то решением будет также функция

где С и С2

Уот = Ci yi(t) + C2y2(t), произвольные постоянные.

Теорема 2. Если y(t) — частное решение неоднородного разностного уравнения (20.1) и y(t. Сі, С2, ... , Сп) — общее решение однородного уравнения (20.2), то общим решением неоднородного уравнения (20.1) будет функция

y(t) = y(t, Си С2, ...,Cn) + y(t),

где Сі, С2, Сп — произвольные постоянные.

Эти теоремы сходны с теоремами для дифференциальных уравнений.

Системой линейных разностных уравнений первого порядка с постоянными коэффициентами pij называется система вида

Yt = PYt.1 + Fu

где Yt =

3/2 (<)

вектор из неизвестных функций,

Ff =

h (t)

fn(t)J

вектор из известных функций,

р =

/Pll Pl2 Р21 Р22

Рп1 Рп2

Р1п Р2п

Рпп/

есть матрица размера п х п.

Эта система может быть решена сведением к разностному уравнению п-го порядка по аналогии с решением системы дифференциальных уравнений.

14 Я. М. Ахтямов

20.2. Решение разностных уравнений

Решение разностного уравнения первого порядка.

Рассмотрим неоднородное разностное уравнение

yt-ayt-i = f{t). (20.3)

Соответствующее однородное уравнение есть

yt-ayt-! = 0. (20.4)

Проверим, будет ли функция

ytoAu = а1

решением уравнения (20.3). Имеем

Vt-i одн = а*-1. Подставляя в уравнение (20.4), получаем

а1 -аа1~х = а1 а1 = 0.

Следовательно, yt 0дн — есть решение уравнения (20.4). Общее решение уравнения (20.4) есть функция

У t одн — С а1,

где С — произвольная постоянная.

Пусть yt — частное решение неоднородного уравнения (20.3). Тогда общее решение разностного уравнения (20.3) есть функция

yt = ytom + yt = Ca +yt.

Найдем частное решение разностного уравнения (20.3), если f(t) = с, где с — некоторая постоянная.

Будем искать решение в виде постоянной т. Имеем

yt = m, yt-i = т.

Подставив эти постоянные в уравнение

yt ayt_x = с,

получаем

т — am = с,

откуда

Следовательно, общее решение разностного уравнения

Уг ~ ayt-i = с

есть

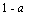уг = Са* +

с

V Пример 1. Найти с помощью разностного уравнения формулу прироста денежного вклада Л в Сбербанке, положенного под р \% годовых.

Решение. Если некоторая сумма уо положена в банк под сложный процент р, то к концу года t ее размер составит

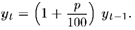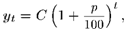Если принять уq = А, то С = Л, откуда

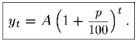Решение разностного уравнения второго порядка. Рассмотрим неоднородное разностное уравнение второго порядка

yt+pyt-i + qyt-2 = f(t)

(20.5)

и соответствующее однородное уравнение

Уг +РУі-і + ЧУ1-2 = 0.

(20.6)

Если к ф 0 является корнем уравнения

к2 +р к + q = 0,

(20.7)

то функция

У t одн

= к

t

есть решение однородного уравнения (20.6).

Действительно, подставляя к1 в левую часть уравнения (20.6) и учитывая (20.7), получаем

к1 + pkt~1 +qkf-2 = kt-2(k2+pk + q) = 0.

Таким образом, если к — корень уравнения (20.7), то к1 — решение уравнения (20.6).

Уравнение (20.7) называется характеристическим уравнением для уравнения (20.6).

Если дискриминант р2 — 4q характеристического уравнения (20.7) больше нуля, то уравнение (20.7) имеет два разных действительных корня к и &2, а общее решение однородного уравнения(20.6) имеет следующий вид:

УюАн = Сг к! + С2Ц.

Общее решение неоднородного уравнения (20.5) таково:

Vt = Vt одн + Vt = Сі к[ + С2 к + yt,

где yt — частное решение неоднородного уравнения (20.5), а С и С2 — произвольные постоянные, которые можно вычислить по начальным условиям, например, у(0) = уо, у(1) = у.

V Пример 2. Найти решение разностного уравнения второго порядка с постоянными коэффициентами

Уг "5ш-1 +6^-2 = 7,

удовлетворяющего начальным условиям

Уо = 5, у = 9.

Решение. Характеристическое уравнение для соответствующего однородного разностного уравнения таково:

k2 -5к + 6 = 0.

Корни уравнения к = 2, к2 = 3 действительны и различны. Следовательно, общее решение однородного разностного уравнения есть функция

yt = Сі2* + С23*.

Предположим далее, что yt = c есть частное решение неоднородного уравнения, тогда

с — 5с + 6с = 7,

откуда

2с = 7; с=-.

Таким образом, общее решение заданного неоднородного уравнения есть функция

yt = Cl2t + C23t+7-.

Постоянные С и С2 определяем по начальным условиям Уо = 5, у = 9. Для t = О и t = 1 соответственно получаем

5 = С12° + С23°+7-, 9 = С121 + С231+7-.

Решая систему уравнений

2 Сі + З С2 =

11

находим

Сі = -1, Поэтому в итоге имеем

Со =

Математика — это искусство давать разным вещам одно наименование.

Анри Пуанкаре