Глава 3 предел последовательности 3.1. понятие сходимости

Глава 3 предел последовательности 3.1. понятие сходимости

Определение. Последовательностью называется числовая функция /(п), заданная на множестве натуральных чисел N.

В дальнейшем вместо f(n) будем писать ап.

Если п — натуральное число, а ап — значение последовательности в точке п, то говорят, что п называется номером числа ап, а само число ап называют общим или п-м членом последовательности. Для последовательности с общим членом ап употребляются следующие обозначения:

an, п = 1, 2, 3...;

КО;

{ап} •

Графиком последовательности является изолированное множество точек плоскости.

V Пример 1. Даны последовательности:

ап = а = 1, 2, 3...;

п

оп = (-1)п, п = 1, 2, 3...;

ап = п — 2, п = 1, 2,3....

Изобразить несколько первых ее членов на координатной плоскости.

Решение. Придавая п значения 1, 2, 3, 4, 5, получим: 11111

ах = -. а2 = -, а3 = -. а4 = аъ = -;

ai = -1, а2 = 1, а3 = -1, а4 = 1, аГ) = -1;

аі = —1, а2 = 0, = 1, = 2, а5 = 3.

Графики этих последовательностей изображены на рис. 3.1. А

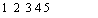
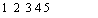-1

х

н—і Т Т Т

1 2 3 4 5

3-2-1 

-1

х

х

Рис. 3.1. Графики последовательностей

V Пример 2. Пусть в момент времени п цена на товар со-1

ставляет ап = 1 Н— денежных единиц. Определить к какой цене п

стремится цена на товар с течением времени.

Решение. С ростом номера п число ап (n-й член последовательности) становится все ближе к 1. Действительно, разность ап — 1| (расстояние от ап до 1) приближается к нулю:

при п = 1 равна |1 + 1 — 1| = 1;

при п = 2 ап 1| = |1 + 1/2 1| = 1/2;

при п = 3 ап — 1| = |1 + 1/3 — 1| = 1/3;

при п = 4 ап 1| = |1 + 1/4 1| = 1/4;

при а = 10 ап 1| = |1 + 0,1 1| = 0,1;

при п = 100 ап 1| = |1 + 0,01 1| = 0,01;

при п = 1000 ап 1| = |1 + 0,001 1| = 0,001.

Легко заметить, что:

при п > 1 имеем ап — 1| < 1;

при п > 10 имеем |ап — 1| < 0,1;

при п > 100 имеем |ап — 1| < 0,01;

при п > 1000 имеем ап — 1| < 0,001.

Таким образом, с течением времени цена на товар падает и приближается к единице. Единицу именуют пределом последовательности изменения цены товара. А

Приведем более точное определение предела.

Определение. Число а называется пределом числовой последовательности {ап}, если для любого, даже сколь угодно малого положительного числа є > 0, найдется такое число N (зависящее от є, TV = TV (є)), что для всех членов последовательности с номерами п > N верно неравенство

а < е.

(3.1)

Если это выполняется, то пишут hm ап = а или ап а при

П —> ОО.

Обозначение lim — сокращение от латинского слова limes — «предел» и равнозначного французского слова limite.

Последовательность, имеющая предел, называется сходящейся, в противном случае — расходящейся.

Используя логические символы V (вместо фразы «для любого»), 3 (вместо слова «найдется») и символ равносильности определение предела можно записать в виде

(а = lim ап) О (Ve > О 3N Vn > N ап а < є).

Смысл определения предела числовой последовательности состоит в том, что для достаточно больших п члены последовательности {ап} как угодно мало отличаются от числа а (по абсолютной величине меньше, чем на число є, каким бы малым оно ни было).

V Пример 3. Пусть ап = 1 + —. Доказать, что lim ап = 1.

Решение. С ростом номера п число ап (n-й член последовательности) становится все ближе к 1. Действительно, разность ап — 1| (расстояние от ап до 1) приближается к нулю. Более

строго, для любого є > 0 выберем число N равным -. Отсюда

1 1 1 6

для любого п > N = имеем: а > или — < е. Но ап — 11 =

І І є en

= 11 Н 11 = —. Поэтому ап — 11 < є. Таким образом,

п п

Ує > О 3N (N = -) Vn > N ап 11 < є.

є

Это и означает, что lim ап = 1. А

V Пример 4. Дана последовательность

а = 0,3, CL2 = 0,33, аз = 0,333, ... .

Доказать, что lim ап = .

Решение. Общий член последовательности ап неограниченно приближается к -. Действительно, разность ап — последовательно равна

11 11 11

3 30' z 3 300' ^3 3000' т. е.

_ 1 _ _ 1

ап~ з ""гГйР

Неограниченность приближения ап к ^ выражается в том,

_^ о

что абсолютная величина разности ап , начиная с некоторого

о

номера остается меньше любого (заранее заданного) положительного числа є. Так, если задать є = 0,01, то N можно выбрать равным единице, поскольку начиная со второго номера (п > N), абсолютная величина остается меньше 0,01. Если задать є =

= 0,005 ^= •> то по-прежнему можно считать, что N = 1.

Если є = 0,001, то N = 2; если є = 0,00001, то N = 4 и т. д. А

V Пример 5. Показать, что число 2 является пределом по(-1)п

следовательности ап}, где ап = 2 Н .

п

Решение. |ап — 21 = —, а величина —, начиная с некоторого п п номера, остается меньшей любого заранее данного положительного числа є (если є = 2, то начиная с первого номера; если є = 0,02, то с 51-го и т. д.). А

Пример 5 показывает, что члены последовательности могут быть то больше, то меньше предела. Они могут и равняться пределу (см. следующий пример).

V Пример 6. Показать, что последовательность 0, 1, 0, ^, 0,

1 і 1 (-1Г

общий член которой выражается формулой ап = —| ,

З п п

имеет предел b = 0. А

Решение. Величина ап — 0| =

і + (-і)"

п п

начиная с неко-

торого номера, остается меньше любого сколь угодно малого по/ 1

ложительного числа є (если є = -, то начиная с седьмого номера;

о

если є = 0,01, то с 201-го и т. д.). А

V Пример 7. Показать, что последовательность ап = (—1)п не имеет предела.

Решение. Члены последовательности а± = — 1, а<х = 1, аз = — 1, а4 = 1 и т. д. не стремятся ни к какому числу. Действительно, какое бы число мы ни предложили в качестве предела а при є < 0,5 неравенство ап — а < є, определяющее предел последовательности, не удовлетворяется. Вне є-окрестности этого числа остается бесконечное число элементов ап. А

В определении сходимости и предела последовательности нет ясного указания на то, как проверять сходимость и как находить предел. Поэтому для вычисления пределов используются специальные критерии. Этим критериям и посвящен следующий параграф.